“To Count” can mean two things.

The first meaning is to point to a thing and say the number 1, then point to the next thing and say the number 2, then point to the next thing and say the next number, and continue doing this until all the things have been pointed to and labeled with a number.

The second meaning is to be important.

A lot of math can be performed by counting. Now bear with me while I explain how.

To add two numbers you can go out and gather a bunch of things, hopefully easy to pick up, and count out a group with the first number of things, then count out a second group with the second number of things, then combine the two groups and count the combined group’s number of things.

To subtract two numbers you can count out a group with the first number, then, out of that first group, count out a second group with the second number. After taking the second group away, count how many remain in the first group.

To multiply two numbers you can count out a group of the first number, then make more groups of the same number, counting out the second number of groups. Then combine the groups and count the combined group’s number of things.

To divide two numbers you can count out a group of the first number, then start dealing out the things like a deck of cards among the second number of groups. Once you run out of things to deal out, you count how many things are in each group.

The reason I have explained how to use counting to do math is because to me, it was hard-won information. I went to a public school that did a little experiment in my class, called Open Classroom. The principal was very much against this type of classroom, but boy did I love it. To this day, it is my memory of my favorite study environment. Open classroom means you as a student can choose what area of the room you want to be in – whether the reading carpet area surrounded by book cases (oh yeah), the workshop corner (where you could only go to on Thursdays when a part-time teacher would be there ready to help you saw wood), the science area where sometimes a teacher would be available to let you play with the guinea pig or to poke at the monarch caterpillar cocoons if they were in season, the picnic table on the other side of the bookcases used as the writing area, or the other picnic table on the other side of room used as the math area.

Now here is where I will make a little observation of open classroom. If a six-year old in an open classroom doesn’t understand the teaching methods used to teach a subject, that six-year old will avoid those teaching methods in the easiest way made available – by avoiding the subject. So, if you are going to be doing some experimental type of classroom like Open Classroom, you better also allow choices for how to learn a subject, not just choice as to whether or not to learn the subject.

Alas, the math picnic table did not offer me the option to learn how to do math by counting. The math picnic table instead only provided one teaching method for math: Cuisenaire rods. Cuisenaire rods are these awesome rods that are like measuring sticks with no markings. There are ten different sized rods, ranging from 1 centimeter to 10 centimeters long. Each length is a different color (1 centimeter rods are always white, 2 centimeter rod are always red, etc.).

Every kid in existence is able to understand math from using Cuisenaire rods. Except for me.

At the top of this blog is a picture from my notebook from a day when I have wandered over to the math picnic table.  The date is September 15. It is still relatively early in the school year. I have spent the first two blissful weeks of school on the carpeted reading area, doing nothing but reading. Today I hear that there is a teacher in the woodworking area, so I decide to explore something new. I do some dangerous stuff in that dark and mysterious woodworking corner, then I try my hand at writing composition, then I check out the Guinea pigs. Next to the Guinea pigs is the math picnic table. For whatever reason, I go sit down there, acutely aware that the students sitting there probably have a two week head-start on whatever it is that is being explained here. I distinctly remember writing down what the teacher was demonstrating, and leaving the picnic table completely baffled. How are two sticks equal to 19? What is 19? Do I have to memorize which color combinations make 19? I decide not to visit the math picnic table anymore. I do not learn how to add. I certainly do not learn how to subtract. And when my parents decide to move to a different state in the spring of that school year, I enter a new public school and am given a subtraction test.

I am staring at the subtraction test and I realize I have never learned subtraction. I hide my hands under the desk and start using my fingers, and I am ashamed. I am trying to figure out how to do subtraction all by myself. When I was very young, before I ever went to school, I remember my older brother bragging that he had figured out how to use his fingers to add – figured it out all on his own – before he ever entered school. I must have been four at the time, and I had never added on my own fingers – I had never seen the need for it – and I figured that I would be taught how to do so when I entered school.  Well, by age six sure enough I did see the method here and there from friends, along with the ridicule that it is a baby method. I knew nobody else doing the math test was using their fingers – I had the sense that it was against the rules.

Which brings me to the second definition of “to count.” Importance. Why were some Cuisenaire rods of different lengths and colors more important than others, so that they counted more? Why was using my fingers to subtract so forbidden? Why was math so mean? It made me ashamed. And why did it have to throw so many numbers at me, like weapons or threats?

To illustrate why so many of us have a fear of math, I would like to steal from material from a Ted Talk given by Dan Meyers.

He gives the example of a math problem:

And then he gets rid of the numbers. The only writing that remains is: A water tank… how long will it take you to fill the tank?

And then he gets ready to count the minutes:

But counting is tedious. So as the students are waiting for the tank to fill up, he asks them for their guesses.

And guesses are something that anyone can engage in. Suddenly, the students who are intimidated by numbers are on the same level playing field as the rest of the class. So for the first time, these students start participating. And as the discussion opens up, suddenly the students start realizing that they could guess a lot better if they had more information: how tall is the tank? How wide around is it? How fast is the water flowing? And only then, when they ask for the numbers, are they given them.

So the second definition of to count is also an impediment. When too many things are made important, stressed, and it is not clear why those things are important, a person feels overwhelmed. You would think, that after all my ranting about counting, that I would say counting is the way to teach math. But really, the irony is that counting isn’t important in teaching math either.

When I was 23 I got a job teaching two year-olds. Part of the curriculum was to teach them to “recognize quantities up to 10.” I started out by teaching them to count, but the headmistress of the school took me to the side and said, “no.” She told me that I was to teach them to recognize quantities BEFORE I taught them how to count. She said that the mainstream way to do is wrong – as in backwards – as in kids are always first taught to count in order to recognize quantities. But kids can recognize that two objects are two objects just by looking at them, she argued – they don’t need to count to do that. Same with three objects, same with four. Get the kids to recognize objects up to 10 BEFORE they learn how to count. Teach them the word for larger and larger amounts of objects, but don’t point out each one, labeling each one with a number to get to the final number. Just tell them: this is 5. This is 6. See if they can tell you how many they see. The kids that she taught to really get a sense of how many or few items were in front of them, she said, never had trouble with math in the future.

I have to agree that what she said makes a lot of sense. If you ever watched a two year-old or even a six year-old count, it is a painful thing. They don’t do it methodically, they point to objects but don’t think of moving or grouping or indicating they have counted the objects, so that they inevitably double count or skip an object. On top of that, they often forget what number they are on or don’t know the next number, or go from seventeen to seventy.  If they only had a sense of how large or small a number was, they would know they didn’t have seventy objects when they really had seventeen: it just wouldn’t “look” right. Also, if they knew what five objects looked like, they would know in their bones that there is a group of two plus a group of three that make the “look” of a group of five.

Now I will make a confession – I never did get a two year old to recognize more than four objects by glancing at them, nor did I get a two year old who could maintain an attention span long enough to practice the skill. I invented the “Duplo-castle game” where they had to guess the right number of Duplos placed in front of them in order to be able to take them to make a castle. However, a two-year old will tolerate such a game for only so long before realizing that there are many times and other places to access Duplos and play with them that don’t require jumping through such hoops. Five year-olds do a lot better in guessing quantities solely for the challenge of it, though they usually cheat by counting, since they are so determined to give the right answer, and not be wrong.

It is a hard lesson to teach someone that guessing is a skill, and that performing mindless functions to get the right answer is not a skill. A calculator will allow you to give the right answer. But knowing when the calculator’s answer is ridiculous and to doubt it enough to investigate if there was a user entry error or a program bug – that is a skill.

So many clients are scared to do accounting or fill out government forms. It has to do with the basic fear of counting. Fear of adding wrong, subtracting wrong, multiplying and dividing wrong. (Sorry, there isn’t any higher math in accounting that is needed than these four functions.) Even though calculators can do these four functions, clients are simply scared of the numbers. I know what it feels like to have numbers thrown at me, to have methods thrown at me that made no sense, to have methods forbidden that were my only grasp on sanity.

When looking at a government form, the importance of the form is not given, the rational for each question is not given. It takes years of accounting classes before understanding the government’s problems, their thought-process, their needs, and why they ask what they ask and calculate they way they calculate. Their questions can be ambiguous – and the punishment for misinterpreting their question the wrong way can seem unfair. It certainly creates job security for accountants, who have learned throughout the years how to interpret the question.

Before you discount this topic as having nothing to do with accounting, please pause. The intention of this site is an improved understanding of accounting.

If you are working in an accounting office, your first few days are going to be at the mercy of the current staff, and their arrogance or consideration towards you will make a big difference. There is a steep learning curve involved, and the added stress of being subjected to a rude or derogatory attitude does not help. For example, in simply learning what system is being used to save files, there is the assumption that you should know the system, when logically that is impossible: every accounting office has its own unique filing system.

If you are a client, then you will be at the mercy of the accounting staff probably every time you encounter an accounting office, and most likely the learning curve will begin anew each year you meet with your accountant. The more you avoid such meetings, whether due to expense or just plain unpleasantness, the more you will forget and need to re-learn the next time you meet.

Love and manners are the sequel to accounting and arrogance. This is not to profess that they are the solution to arrogance, it is simply to say that love and manners are another black hole in the accounting world, that few people discuss, and that I would like to hear people’s perspective on. Do people like their accounting peers? Do people who work in accounting have good manners? What are people’s experiences? What reasons are hypothesized for those experiences?

Also, the pairing of love and manners does not profess that one is an evolution of the other, like love and marriage.

I think back to English literature I studied in college:

Love is the fart

Of every heart;

It pains a man when ’tis kept close,

And others doth offend when ’tis let loose.

– Sir John Suckling

Or I find thoughts like the following, in the book “The Door” by Magda  Szabó, “I had to break her habit of demonstrating her attachment to me by these undisciplined, insane means. I know now, what I didn’t then, that affection can’t always be expressed in calm, orderly, articulate ways; and that one cannot prescribe the form it should take for anyone else.”

So you see, love and manners do not necessarily follow one from the other. I know a lot about love and very little about manners (love is easy: you curl up on the couch with your cat or your family member and that is love. You lean back and laugh uproariously at the dinner table or run to the door when someone is arriving. When you lack people to love, you are painfully lonely. When you have people to love, you take them for granted.) Manners is a different story. You can love and enjoy someone and yet smother them or lash out at them – very bad manners. You can be misunderstood by someone you had the best of intentions for.

So what are manners? Manners, to me, are telling a patient who is being neglected during triage, that they can’t be helped at the moment.  There are several choices of what you can tell them: other patients are more important, your injury isn’t life-threatening, I am not authorized, this is not my assigned role, this is not the protocol, you are causing problems. And in the stress of triage, these are the things that we often blurt out in desperation. And don’t think that these things aren’t said in an accounting office – whether to other staff or to the clients. But the intention of triage is to provide the most life-saving to the greatest number of people – an act of love.

And in periods that are not emergencies, communication can also fall flat and offend. Humor is the most loving of all communications, in my opinion. Humor shows that you are trying to make someone happy, show someone your vulnerabilities, set someone at ease that there are no formalities that you expect. And yet in the attempt at humor, the recipient of humor is often offended.

I am going on the assumption that people in an accounting office are not spiteful people, that they do not intend to hurt other people’s feelings. I am assuming that people in an accounting office actually feel love for, and care for, their fellow human beings. I am assuming that if people in an accounting office learn proper manners they will be happier, since it is their intention is to make people feel important, loved, and set at ease.

I would like to open the floor up for discussion regarding a topic that often bewilders me. Perhaps someone out there can shed some light on the causes and cures for arrogance in the profession of accounting.

While there are many professions that lend themselves to arrogance, I have found that the arrogance of accountants is somewhat like the arrogance of upper-class housewives (status conscious), actors (bullshitters), and grammar teachers (criticizing others). Indeed, in a case of the pot calling the kettle black, I am sure my rant will illustrate how I display every one of these types of arrogance myself. Contrast the arrogance of your average accountant with, say, the down-to-earth advice and help provided by your average wilderness survivalist. (Don’t be fooled – just because I have pictures of wilderness survival on my blog doesn’t mean I know squat about wilderness survival. More about squatting in the wilderness will be in a later blog).

I believe there are many causes for this arrogance. One cause may be that accounting revolves around money, and money is a status symbol.  Accountants don’t just take unnecessary pride in how much money they can control, but they also put on airs regarding how well they can manage their own money. And this status arrogance isn’t unique to those accountants who actually do make a lot of money. Bookkeepers are extremely susceptible to this type of holier-than-thou arrogance. Bookkeepers can survive on a shoestring budget, and they simply can’t understand how their clients, who rake in tens of thousands a month, can be in huge debt and constant overdrafts. (More about why bookkeepers find it easy to survive on a shoestring budget will be in a later blog.)

Another cause may be that run-of-the-mill accounting work is extremely easy, in extremely high demand, and most accounting jobs require neither a college education nor a CPA certificate. This may seem counter-intuitive – why would a ubiquitous, easy job lend itself to arrogance? It is easy for ignorant people to get a job in accounting, and ignorant people, after they get what they consider an important position, are often arrogant.

When I was getting my accounting degree, in the freshman classes, students would raise their hands quite quickly and loudly comment on hypothetical case studies. Everyone was so sure of themselves, and most of the class was currently working in some sort of low-level accounting job. By the time we all got to our senior year nobody raised their hand quickly anymore, and we wouldn’t have even if we had been presented with the exact same hypothetical case studies that we nailed as freshmen. When we did answer, our wording would be more along the lines of “I’m not sure, but perhaps…”

Using this logic, the most uneducated are the most arrogant and the most educated are the least arrogant. Sadly, it’s not so simple. Your best employee may be a fourteen-year-old high school student who comes in after school with no attitude, a sponge eager to learn. Your worst employee may turn out to be a CPA or other highly educated or experienced person who doesn’t want to learn something new or won’t change their set ways and who would never listen to the suggestions of a high schooler.

Another cause may be because accounting can be a fuzzy subject, and so requires a bit of bluster to make others believe in the correctness of a position. Accounting is not supposed to be fuzzy, and it is illegal to do it incorrectly. However, there are many legal areas that allow options, estimates, exceptions, and judgement. Consider the following definitions found in the tax standards:

Will	Generally 90% or greater probability of success if challenged by IRS
Should	Generally 70 – 80% probability of success if challenged by IRS
More Likely than Not	Greater than 50% probability of success if challenged by IRS
Substantial Authority	Weight of authorities in support of a position is substantial in relation to the weight of authorities in opposition to the position (40%)
Reasonable Possibility of Success	1 in 3 possibility of success if challenged by IRS
Reasonable Basis	Significantly higher than not frivolous and lower than realistic possibility of success
Not Frivolous	Not patently improper; some merit to position
Frivolous	Patently improper

https://www.irs.gov/pub/irs-utl/statements_on_standards_for_tax_services.pdf

Because of the fuzziness in the subject, an accountant has to argue a lot. A tax accountant may spend 10% of his or her time calculating the tax and 90% of his or her time convincing the client to pay it, setting up tax installment payments and handling tax liens. Similarly, an auditor may spend 10% of his or her time looking at the financial reports and 90% of his or her time brainstorming, discovering and pointing out how the books are incorrect.

It would be easiest if an accountant allowed all the items a client insisted on, however, an accountant is supposed to serve the public interest, not solely the client. Yet who pays the accountant? The public interest? Perhaps if the accountant is a government auditor. No, for most accountants the client pays the auditor. It is hard to collect money from a client after they perceive that you have destroyed them financially by making them pay taxes or by making their loan application or SEC filing look weak. And while some accountants do bend to the will of their clients, other accountants, who like to cover their ass and keep their license, don’t. So accountants learn to deliver an air of authority, in order to waste as little time arguing as possible.

And when clients, after being intimidated into silence by their accountant, leave their accountant to choose another accountant, usually the first thing the other accountant does is criticize the accounting that had been done by the prior accountant (too aggressive, too conservative, too sloppy, overlooked deductions, too many deductions, red flags for audits, done just plain wrong). It is easy to do – after all, the client is looking for a new accountant and so must have had doubts, besides, accounting is a fuzzy subject so you can always be believed when you say someone else did it wrong. What easier way to establish your authority and impress your client than to point out how you are so much better and smarter than other professionals.

Another reason that accounting may lend itself to arrogance is that there are so many exceptions and exceptions to exceptions, and each industry has its special treatments, that it is not possible to know everything. Plus, the laws and treatments are always changing, so even if you know something one year, you may not know the most up-to-date rule this year. So if you are wise, you feel a little bit of insecurity when you are confronted with something that you need to research. But in the spur of the moment, when someone is asking you a question, do you want to display that insecurity to a client or to an employer or, much worse, to the people under you?

If you are not wise, meaning, if you don’t even know that you don’t know, you may be tempted to just offer the “logical” answer (which often enough is the wrong answer). Say you are a receptionist during tax season, on April 15, and you pick up the phone and it is a random phone call from a frantic person, not a client, who just wants to ask whether filing an extension will extend the deadline to pay the tax. It is so simple to answer what you believe is the logical and therefore correct answer, “of course you idiot, just file your extension because that allows you to pay your tax later.” You are the authority, after all someone asked you a question so they must assume you are the right one to ask, plus your job as a tax office receptionist exposes you to all sorts of accounting paperwork and you have heard jargon, and even if you never specifically heard a rule about tax payment deadlines being extended, you can figure it out “logically.” I mean, it feels good to know it all and give people answers.

Studies have shown that a lot of people have the tendency to answer something even when they know they do not know the answer. Do you know what the three hardest words in the English language are? How many times have you given directions to a stranger to get to a place you were only vaguely familiar with, stating the directions with full authority, without even a hint of ”I may be wrong, and you probably would be better off asking someone else.” In the wilderness, you walk softly and you carry a big stick. In accounting, you do the opposite – walk loudly but really don’t know the answer to the question.

Along with not knowing the answer, accountants often do know the answer. For whatever reason, they must pick on someone else who does it wrong, usually someone whom they shouldn’t expect to know the answer, like a new employee or a client. Accountants forget the years of experience and training that have brought them to the level of understanding they now have. They forget that it takes time and practice for a concept to sink in. Accountants are short on time. They always have deadlines, and can’t afford to be patient when a new-hire or a client doesn’t understand what to do. Many small or mismanaged accounting offices don’t have resources for the un-initiated, and they take their frustrations out on those who know less than them.

So I have offered a few descriptions of types of arrogance. The upper-class house-wife: feeling important because you control large amounts of money. The actor: insecure when you know you don’t know something, and its corollary, hopeful your bullshit will make others think you do know that thing. The grammar teacher: feeling infallible when you know something and its corollary, impatient when others don’t know that thing.

A review course will provide the material you need to learn to pass the CPA exam. Sometimes if something is handed to you, you take it for granted or find fault in it. When you think that a subject is not being taught clearly, or is boring, go find a better source to learn about the subject. Pull out an old text book or search the internet for a better explanation or for examples. One of two things will then happen: 1) either you will get a better understanding or 2) you will realize that the explanation provided by your own course is more helpful than other sources. But more importantly, you will realize that you are your own teacher, not your review course, and it is your responsibility, not the review course’s responsibility to teach yourself. Be grateful for the resources provided by your review course, as you are your own teacher and they are helping you.

Be grateful for the internet. If you don’t understand a practice question, type it word for word into a search browser. The practice questions that your review course provides are from the CPA exam test bank. No matter what review course students are taking, they all most likely are practicing with the same questions. Many other students have stumbled over certain questions, and, unsatisfied with the answers provided by their CPA review course, have posted a plea for help on understanding the question to the world wide web. And thank goodness there are those who like to post answers. There are free resources like Khan Academy that will teach topics in detail, such as economics, stock derivatives, present value calculations.

Look at each answer as you go along when you take a practice test. This can go against the grain for some people who don’t think they will be able to assess themselves if they cheat by looking every few minutes, or who are too proud to need to look at the explanation. It is no more cheating than answering a professor’s question in class and getting immediate response as to whether you are right or wrong, and why. You will learn more from the answers you get wrong than from the answers you get right. You can learn a lot by getting immediate feedback on your wrong answers, and get them out of your system before exam day. Your goal on exam day is total confidence about your answers.

Be interested in what you are learning. If you have been lucky enough to have been close in your life to people who were bona fide geniuses, you may have noticed that they had an interest in things they studied. Sure, exterior motivation can make grades a game, competition can make a person exert more effort, fear can prevent someone from not doing their work, and inspiration from a good teacher can make things interesting, parental guilt can make one behave, but these are all exteriorly imposed interests. While genius comes in all forms and personality from humble to braggart, from well-intentioned to twisted, from quiet to loud, genius does have in common an element of interest in what is being studied. If you have not ever had geniuses in your life, then look around you at people you know that have certain traits or strengths. Even if these people aren’t all-around geniuses, think about those traits they are good at. Indeed, especially since those people are not geniuses, for them to be good at certain things required them to be interested in those things.

So while many people will tell you to motivate yourself by envisioning yourself with the three letters CPA on a placard or a certificate on your wall, or the envy of your friends, or sticking it to your boss or escaping your life of drudgery or pleasing your family, realize these things are exteriorly imposed interests. Realize these things will motivate you but they won’t help you understand what you are studying until you actually can find something about the materials that is interesting. One of the best ways to get interested in the materials is to practice the Task Based Simulations. The biggest benefit of practicing the TBS sections of the homework is not necessarily “to prepare you for the TBS section of the exam.” Instead the biggest benefit is to 1) give you a vision and example and allow you to imagine how the information is used in real life which in turn will 2) interest you in the subject and your interest will in turn 3) allow you to learn the subject in a deep way.

The math on the CPA exam is about 4^th grade level – almost all the percentages are 10%, almost all the numbers are an even million. The calculator isn’t necessary, it is just there for security and a sense of order and as a record of the numbers and operation that you have performed, so you can check your work. In most problems you can do the math in your head faster than the time it takes to type it into the calculator.

Be aware that accounting is about imagination, not math. This is the key to getting interested in the subject or the problem. You look at numbers and you see in your mind’s eye a warehouse, with shelves loaded with boxes of inventory, and a loading dock and a grisly old warehouse manager with crumpled, coffee stained receiving reports piled up on his desk. You look at numbers and you see a drafty, echoing manufacturing plant, with crowded store-rooms of raw materials, and stations in various stages of unassembled parts, welders, metal dust, noise, forklifts, the time card clock, benches of technicians.  You look at an org chart and you see glass offices with long desks and executives behind a monitor, a phone, memorabilia, post-its, white-boards, file folders, books, a visitor’s chair; you see the executive getting up, roaming the halls, rubbing elbows, bringing blue-prints or plans or reports to other executive’s offices.

It is sometimes hard to get a picture of what is happening when you see a practice question that starts in the usual sterile way: Hall, CPA is engaged to blah blah blah. All your mind’s eye may be envisioning is a cold, empty walled (ok fine, maybe there is a portrait of the firm’s ancient founder) accounting office with unfriendly clients, uncomfortably formal clothes and no joking allowed.  But why can’t Hall, CPA be an accounting office with 70’s art and a throw rug with a receptionist who decorates the reception area with crystal balls and beads and an alcoholic boss and the clients are crying wives and young entrepreneurs.  Why not? Not that you would want to work there, but it is a more interesting question that way.

If you find yourself looking at a concept that you have to learn and recoiling with the thought “I will never use this knowledge in my life, I am just going to close my eyes, hold my nose and swallow it and then regurgitate it on the exam” you are missing out on interest. If studying auditing is boring to you, watch some tv crime shows where you see the FBI interrogate suspects, find clues, uncover plots. If studying BEC is boring, find some purchases you may want to buy, compare them as to their useful life and the value they will provide versus their opportunity cost. If studying REG is boring, get into a contract with someone and find out how important it is to know the law when the person turns out to be a crook.  You are only limited by your imagination when dreaming up “will this knowledge ever be useful or entertaining to me.”

Do not think that what you learned in college will get you through the exam without a review course. What you learned in college may be obsolete by the time of the exam. Just because you had to do a whole research project in school on what is considered an extraordinary event doesn’t mean that the rules can’t change by the time you get out of school, and suddenly the whole concept of extraordinary events that you learned in college has been trash-binned. Do not think that what you learned in the workplace will get you through the exam. What you learned in the workplace may be, or probably is, different than the ideals the exam tries to test. Just because your accounting office allows a self-employed person to have losses year after year, and successfully defends those losses in IRS audits, doesn’t mean the exam won’t expect you to treat such activities as hobbies. Do not think that the review course infallible, especially the lectures. Sometimes the lecturer will mis-speak without realizing it, you need to be able to question concepts that do not make sense, use the internet and see if the concept can be clarified, and not be angry with a course that allows materials to be presented imperfectly. It is up to you to learn what you need to learn, whether your sources are correct or not. When in doubt, you can always read the authoritative literature, access to which is provided free to CPA exam candidates. You will find that your review course has actually done a very good job of presenting what you find to be written in Greek in the authoritative literature.

Design your own teaching tools and lesson plans. You know yourself best, make your activities something that you know you will learn from, not something that will put you to sleep.  It may be as simplistic as reading a chapter and doing 30 multiple choice questions a day.  Or it may involve note-taking, flash-cards, listening to videos. At one point I got frustrated with the randomness of the questions of my computerized review course. I wanted to be able to flag certain questions in a more efficient manner, and be able to be asked certain questions over and over that I felt to be good at teaching a concept, and I wanted to avoid other questions that I felt were a waste of time because they were too easy and too time-consuming. I wasn’t satisfied with the flagging ability of the software, which I found too clumsy. So I started to painstakingly copy and catalog each question into a word document. It was an extremely laborious task, but the end result was that I had access to all the questions, organized and flagged with the symbols I could use to locate and ask myself the questions that I found the greatest teaching questions.

Even though everyone learns differently, I believe that certain actions are indispensable, and that quite possibly if you do not do these actions you will not pass:

• Take notes and/or create your own flash-cards. I prefer flash cards because they force you to distill the essence of a concept and are easier to review later as refresher. Writing notes serves the important function of forcing you to pay attention to what you are studying – you find that sections you glossed over or day-dreamed through suddenly make sense and come into focus.
• Do the practice questions
• If your text book is more than a year old, check that the information is not obsolete or superseded. Sometimes the lectures online will have information that contradicts the text book you are studying – and the reason may be that the lectures are up-to-date but your text book is old. Ask your review course to send you any errata or text-book updates. (Sometimes of course, the lectures simply have a lecturer who mistakenly says the wrong thing, so the text may be right). The point is to be very careful if the text is even one year old. Accounting standards are constantly converging, being re-organized, clarified, changed.

When watching a video or reading about a concept, if you find yourself not paying attention, do not go further. Re-wind or re-read. Most likely you will again wander off. Stop and re-wind as many times as is required for you to pinpoint what you have been glossing over. After you have pinpointed what it is, learn it. If you really cannot learn it, then make a note to yourself to come back to it later, after you have gained a wider foundation by learning the rest of the course. Do not discount the value of learning anything, or make the decision not to learn it. Note the area. Take the time to understand it or make the effort to come back to it later.

If your videos provide the ability to speed up or slow-down the video, play with the speed.  If you have heard the lecture many times, reviewing it at double speed will help you review without boring you.

Learn the basics before getting into the details. This often requires a spiral approach, going through the entire course and all the materials and then starting at the beginning again to fill in the gaps or the things that you may not have grasped fully the first time around, or that you forgot.

Use practice questions as a learning process, not as a critique. Areas that were hazy when you were reading or listening to them will begin to make sense as you do the practice problems. Don’t be worried if you get most of the problems incorrect your first couple times through them. Your score on the practice problems when you are first learning the material has absolutely no correlation with what your score will be after you understand and start to master the material.

Take seriously the amount of time it takes to learn the materials. It takes several hundred hours. When you hear someone tell you that all they did was lock themselves in a room and study intensely for one weekend and passed, understand that the truth may be a bit different. What probably was the case was that they were carelessly reading the material for months and weeks, watching tv, taking days away from the materials, not taking their studies seriously, when all of a sudden the seriousness of their situation (as in, their scheduled day for the test) forced them to focus intensely.  There is nothing like the enormity of the deadline to force a person to focus.  And it is true, a weekend of focus will get you through the exam. However, realize that IF the person passed it is BECAUSE the person DID look at the materials for weeks and months before that “one weekend of studying.” Those months and weeks of careless reading or thumbing through the materials were actually laying the foundation and allowing the person to mull over concepts, get used to terminology, get familiar with the subject. There is no way to pick up the materials for the first time and focus in one weekend. Do not believe it. Do not try to do it. That is the reason the majority of candidates fail. It is expensive, it is a lie that it can be done that way, it is a brag that you will regret believing, don’t believe it.

Be willing to change your approach, study style, and type of skill for each section. While concepts overlap, treatment of those concepts differ, so do not get stuck in a rote expectation of how to answer a question. In FAR you may be asked to calculate or present a derivative, in BEC you may be asked to write an explanation about how derivatives work, in audit you may be asked to look at the risk factors of derivatives.  So don’t blow off studying a topic because you think you know everything about it from a different section, or because you think it will only be tested in a certain section. Have the humility to look at it again.

The research database for FAR has only be one set of standards to search through (FASB).  However, AUD has a whole array: at, ar, ar-c, et, bl, cs, qc, pr, pfp, cpe, pcaob, ts, vs, au-c. So while just being able to use search skills may carry you through FAR, AUD requires you also know which database is which. Don’t assume just because you were proficient with a concept or task when taking section of the test that you won’t have to study or practice it in a different way when you take a different section.

Another thing different about the research in AUD versus the other sections is that the AICPA clarity standards organize each standard with the following sections:

Intro

Objectives

Definitions

Requirements

Application

The standards go on for many pages, so it is easy to lose your orientation as to which section you are in. One hint is that the paragraphs in the application section begin with the letter A.

Look at the research questions carefully to see which section your answer will be in.  Though you may see the same words in each section, you will need to pick the right section based on whether the question is asking for the “definition” or the “auditor’s objective” or “auditor’s procedure.” Also, many paragraphs have what looks like the answer in a short preface, but the subsequent paragraphs give the details that the question looks for.  For example, if the question asks for “auditor’s responsibility for fraud” you may search and find a paragraph titled “Responsibility for fraud.” It may be tempting to choose that paragraph. However, upon closer inspection, the next paragraph is the subsection “Management’s responsibility” and then the paragraph after that is “Auditor’s responsibility.”  It is the third paragraph that is the answer to the question.

In the testing center itself

My own experience with the testing center has so far been very enjoyable. There is a comfortable chair, ample size monitor, mediocre keyboard but at least with number pad, and noise-cancelling headphones. Compared with my own study area at home, on a tiny laptop sitting on a couch or my bed, and millions of interruptions, kids, mess and other people watching tv, etc, the testing area is far more conducive to “getting in the zone.”  If you have been well-prepared you may feel a bit of a high and a sense of effortlessness while taking the exam.

Be sure to go onto the AICPA website and take the test simulation.  Even though your review course has its own simulation, you should still go onto the AICPA website and use theirs at least once.  They have a tutorial that teaches you how to split a screen in half while doing task-based simulations, how to input formulas into their mini spreadsheet answer spaces, etc. The search mechanism in the research questions is different, the calculator is different than in the review course simulations. My first test I took I did not know that I should have tried out the AICPA website and I was disoriented at first by the differences. I was pleasantly surprised by the calculator which was much better than the one I had practiced with during my review course.

Note that the calculator has a check mark that says show tape:

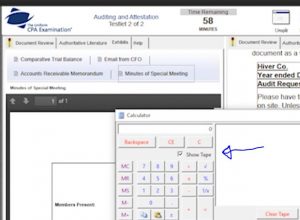
You always want this box checked – be sure not to accidentally uncheck it, or you will miss out on a great tool.

There is also a button that says “Clear Tape” which I recommend that you never touch. Leave the tape alone for the entirety of the test. There are so few calculations that require the calculator that by leaving the tape as a running record, problem after problem, you have a record of your thought process for those few questions that you used it for. This is useful come to back to when you are reviewing your answers before submitting each testlet.

You are provided with two dry-erase laminated graph paper scrap sheets. If you fill up one you can raise your hand and request to replace it with an empty sheet. Be sure to raise your hand ahead of time as you anticipate needing the sheet, since it may take a minute before the test administrator notices you and comes to you. Some people recommend reserving one sheet throughout the test that you have jotted your last minute notes, memory aids, etc on before the test started (there is about 7 minutes of semi-free time that each candidate is allowed before the exam begins – the candidate supposedly is supposed to be spending those 7 minutes reading the contract and rules on the computer, however there is nothing against the rules with using those 7 minutes to write down all the lists, formulas, concepts that you are afraid you may blank out on before you begin the exam.) Many times the two sheets of paper are sufficient for the entirety of the exam (one side for each testlet, max of 4 testlets). I personally write as small and neatly as possible, and number each problem in order to be able to come back to my calculations. However, I have found that I rarely flag a problem to come back to that involves calculations. Usually the only problems that I flag are concepts with no calculations. So even though I have set up each sheet neatly in case I want to revisit, I never actually revisit them. The process of being neat and orderly still has a calming and focusing power.

Be sure to not spend too much time on any one testlet. My first exam (FAR) I went very slowly and methodically through the first 3 testlets because I incorrectly estimated the amount of time I would need on the fourth testlet. I assumed that because there was 4 hours for 4 testlets that each testlet would be on target if done an hour each. I went very slowly, double checking each question several times. I had an hour and fifteen minutes available for the fourth testlet, which I felt was well ahead of target, however I couldn’t have been more deluded. The fourth testlet is composed of 7 task-based simulations which take about 15 minutes each. Being that I hadn’t practiced the format, the first one took some time to get the hang of what they were asking for. The second one as well. After I did the third one, with 30 minutes left, I assessed my progress and realized my mistake in time estimation. By then I really had to go to the bathroom badly, my heart began pounding, and I went into full panic mode, doing the next 4 problems in 5 minutes each. I went back to check over my work, starting at task based simulation number 1, and spending a minute reviewing (and correcting) each one, and when I got to review the last problem I suddenly went blank on the formula (granted I had “known” the formula blindly a few minutes before) but suddenly I started second guessing myself, and started changing all the formulas. Then I triple guessed myself, then quadruple guessed myself, my blood pounding so hard to my brain I don’t know what I was thinking, wildly typing in numbers and having them cascade into each other like dominos, changing them over and over with each realization that there was another element that I needed to change. Finally I changed my last 5 numbers in a row with 5 seconds, 4 seconds, 3 seconds, zero seconds, submitted the damn test and realized that I had changed perfectly good answers for no reason, just because I was in panic mode.

So don’t do that.

One last piece of advice. Don’t listen to anyone who says you are studying too hard and that it is a waste of time to shoot for a high score, since the passing requirement is only 75 percent. Instead, approach the exam like an engineer building a bridge. Over-engineer it, for safety. Shoot for a high score. The exam is extremely expensive.  With four children to support, every hour of study was an hour less of overtime wages, which was a huge blow to my income. I could not afford to fail any section of the exam (could neither afford the cost nor the afford the time to re-study), and so I studied with the goal to get 90 percent on each section, for the margin of safety. I knew there was a high chance I would freeze up on the exam, a high chance I would make stupid mistakes under stress. I wanted the luxury of at least understanding the subject so thoroughly that I would be able to survive being side-swiped by such things.

AUD Score: 97 – Attended: 11/02/2016 12:41:00
BEC Score: 89 – Attended: 07/07/2016 09:08:00
FAR Score: 90 – Attended: 06/08/2016 12:58:00
REG Score: 91 – Attended: 08/11/2016 13:30:00